First Steps
Overview
The basic idea of R/exams is to have a one-for-all exams generator where each exercise is a standalone file, so that the same exercise can be rendered easily into a variety output formats such as e-learning systems or written exams. To reduce the risk of cheating, R/exams offers different mechanisms for drawing random variations of exercises:
- Randomly selecting one (or more) out of a set of exercises for each participant.
- Randomly shuffling answer alternatives in single-choice and multiple-choice questions.
- Randomly selecting numbers, text blocks, graphics, etc. using the R programming language.
Each exercise (or rather “exercise template”) is a standalone file with up to four elements:
- Data-generating process in R.
- Question text.
- Solution text.
- Meta-information: Type of question (single-choice, multiple-choice, numeric, string, or combinations thereof), correct solution, a name/label, etc.
Only the question (2) and the meta-information (4) are mandatory while data generation (1) and solution (3) are optional. Solutions can be used to either inform teachers about the correct solution for some randomly drawn exercise - or for giving students feedback about how to solve a given exercise. Programming a good data-generating process is often the hardest part of authoring a new dynamic exercise but is, of course, crucial for drawing a very large number of random variations.
For formatting the text within question/solution (e.g., italics, bold face, lists, etc.)
two options are available: Markdown or
LaTeX. The former is very easy to learn
and recommended for authors who do not know LaTeX yet. If mathematic notation and
formulas are needed, then LaTeX can be used - either within a LaTeX or also within
a Markdown question. The file suffix for R/Markdown
is .Rmd while .Rnw is conventionally used for R/LaTeX, known as
Sweave.
In the following, a first session should help new R/exams users to explore the materials available and get a feeling for the workflow. Furthermore, two exercise templates are shown in more detail:
- swisscapital: A static single-choice knowledge quiz question where the only randomization is a subsampling of the presented alternatives.
- deriv: A dynamic airthmetic question about the product rule for derivatives where various numbers are drawn randomly in R.
A first session
To explore what is available in R/exams two things are necessary: a couple of exercise
templates to draw inspiration from, and some demo R scripts that illustrate how the
different exams2xyz() functions can produce output in a variety of formats. (Here,
xyz is a placeholder for the output format like html, pdf, moodle, etc.)
The function exams_skeleton() is a helper function that generates exactly these
materials in a specified folder. For example, when exams has already been
installed, the following can be carried out
in R:
library("exams")
exams_skeleton(markup = "markdown",
writer = c("exams2html", "exams2pdf", "exams2moodle"))This copies all R/Markdown files to the current working directory along with demo scripts,
illustrating the usage of exams2html() and exams2pdf() for customizable HTML and
PDF output, respectively, along with Moodle output via exams2moodle(). Specifically,
the working directory then contains:
dir()## [1] "demo-all.R" "demo-html.R" "demo-moodle.R" "demo-pdf.R"
## [5] "exercises" "templates"
Simply open the demo script
demo-all.R for the first steps and then continue with
more details in demo-html.R, demo-pdf.R, or
demo-moodle.R, respectively.
More information about all the exercises can be found in the
exercise template gallery online.
Single-choice: Swiss capital
Knowledge quiz question (about the Swiss capital) with 1 correct and 6 false alternative.
4 out of the 6 false alternatives are sampled randomly and shuffled. Otherwise the
exercise is static and contains no R code. Below the structure of the exercise is
highlighted side-by-side in both .Rmd and .Rnw, illustrating that the additional
exercise markup is similar in spirit to the respective typesetting system.
To see what the output looks like, run the following code within R or take a look at swisscapital in the exercise gallery.


library("exams")
exams2html("swisscapital.Rmd")
exams2pdf("swisscapital.Rmd")
library("exams")
exams2html("swisscapital.Rnw")
exams2pdf("swisscapital.Rnw")
Question
The question is straightforward and lists 7 answer alternatives. The correct solution (Bern) is declared in the meta-information below.
Question
========
What is the seat of the federal
authorities in Switzerland
(i.e., the de facto capital)?
Answerlist
----------
* Basel
* Bern
* Geneva
* Lausanne
* Zurich
* St. Gallen
* Vaduz
\begin{question}
What is the seat of the federal
authorities in Switzerland
(i.e., the de facto capital)?
\begin{answerlist}
\item Basel
\item Bern
\item Geneva
\item Lausanne
\item Zurich
\item St.~Gallen
\item Vaduz
\end{answerlist}
\end{question}
Solution
The optional solution can provide some general feedback (that explains why Bern is correct in this question) as well as more details for each answer alternative (only listing true/false here). It is also possible to have no solution, or just a general text, or just the answer list.
Solution
========
There is no de jure capital but
the de facto capital and seat of
the federal authorities is Bern.
Answerlist
----------
* False
* True
* False
* False
* False
* False
* False
\begin{solution}
There is no de jure capital but
the de facto capital and seat of
the federal authorities is Bern.
\begin{answerlist}
\item False.
\item True.
\item False.
\item False.
\item False.
\item False.
\item False.
\end{answerlist}
\end{solution}
Meta-information
In the meta-information, each exercise must specify at least an extype,
and an exsolution, and should typically also have a short descriptive
exname. The type for single-choice questions is schoice and the
exsolution is simply a binary coding of the 7 answer alternatives.
For randomization, additionally exshuffle is set to 5 so that 1 correct
and 4 random wrong alternatives are subsampled and shuffled.
Meta-information
================
exname: Swiss Capital
extype: schoice
exsolution: 0100000
exshuffle: 5
\exname{Swiss Capital}
\extype{schoice}
\exsolution{0100000}
\exshuffle{5}
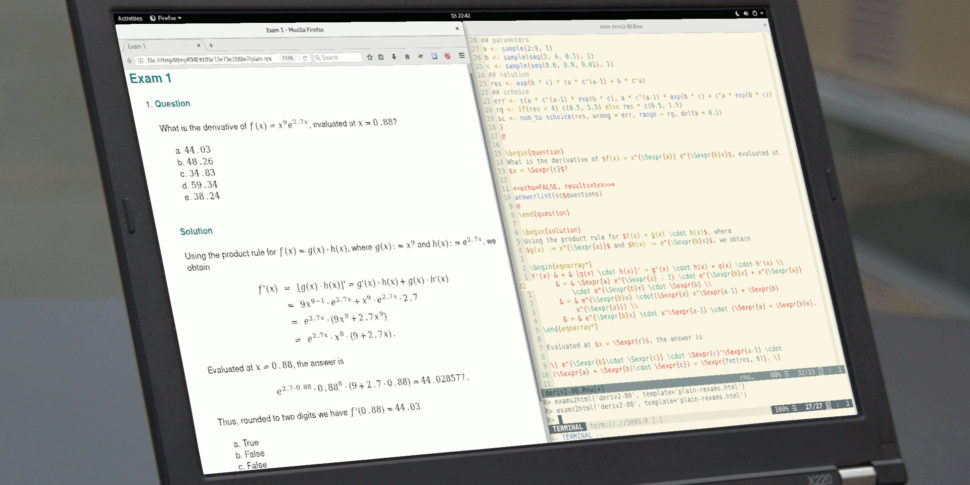
Numeric: Product rule for derivatives
Arithmetic question for computing the first derivative of a product function with two factors, using the product rule. The parameters of the function are drawn randomly in R and subsequently inserted into the question and the solution (which is not shown below for brevity). LaTeX is used for typesetting the mathematical formulas - both in the Markdown and the LaTeX version.
To see what the output looks like, run the following code within R or take a look at deriv in the exercise gallery.


library("exams")
exams2html("deriv.Rmd")
exams2pdf("deriv.Rmd")
library("exams")
exams2html("deriv.Rnw")
exams2pdf("deriv.Rnw")
Data generation
The R code simply draws the two parameters a and b as well as the argument c
from a discrete uniform distribution. (See the question below for the actual function used.)
Subsequently, the random numbers are inserted into the correct solution and storing
it as res.
```{r, echo=FALSE, results="hide"}
## parameters
a <- sample(2:9, 1)
b <- sample(seq(2, 4, 0.1), 1)
c <- sample(seq(0.5, 0.8, 0.01), 1)
## solution
res <- exp(b * c) * (a * c^(a-1) +
b * c^a)
```
<<echo=FALSE, results=hide>>=
## parameters
a <- sample(2:9, 1)
b <- sample(seq(2, 4, 0.1), 1)
c <- sample(seq(0.5, 0.8, 0.01), 1)
## solution
res <- exp(b * c) * (a * c^(a-1) +
b * c^a)
@
Question
The question asks for the derivative of a particular function and simply inserts the parameters drawn above into the question template. (The solution is set up analogously in the exercise template but not shown here for brevity.)
Question
========
What is the derivative of
$f(x) = x^{`r a`} e^{`r b` x}$,
evaluated at $x = `r c`$?
\begin{question}
What is the derivative of
$f(x) = x^{\Sexpr{a}} e^{\Sexpr{b}x}$,
evaluated at $x = \Sexpr{c}$?
\end{question}
Meta-information
Again, the meta-information lists extype (which is num for numeric exercises),
exsolution (which is inserted dynamically from the variable res computed above),
and a short exname. Additionally, the tolerance extol which is used for automatically
evaluating answers, e.g., in an online test/exam.
Meta-information
================
extype: num
exsolution: `r fmt(res)`
exname: derivative exp
extol: 0.01
\extype{num}
\exsolution{\Sexpr{fmt(res)}}
\exname{derivative exp}
\extol{0.01}