scatterplot: Interpretation of a Scatterplot
Name:
scatterplotType:
Preview:
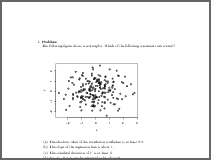
The following figure shows a scatterplot. Which of the following statements are correct?
- False. No association between the variables is observed in the scatterplot. This implies a correlation coefficient close to \(0\).
- False. The slope of the regression line is given by \(r \cdot s_y/s_x\) and hence not about equal to \(1\).
- False. The standard deviation of \(Y\) is about equal to \(1\) and is therefore smaller than \(6\).
- True. The regression line at \(X=0.3\) implies a value of about \(Y = 0\).
- True. The mean of \(X\) is about equal to \(0\) and hence is smaller than \(5\).
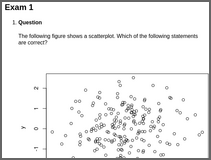
The following figure shows a scatterplot. Which of the following statements are correct?
- False. The slope of the regression line is given by \(r \cdot s_y/s_x\) and hence not about equal to \(1\).
- False. The regression line at \(X=-0.3\) implies a value of about \(Y = -0.1\).
- False. The mean of \(Y\) is about equal to \(0\) and hence is smaller than \(30\).
- False. The standard deviation of \(Y\) is about equal to \(1\) and is therefore smaller than \(6\).
- True. Only a slightly positive association between the variables is observable in the scatterplot. This implies a correlation coefficient with an absolute value smaller than \(0.8\).
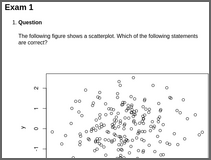
The following figure shows a scatterplot. Which of the following statements are correct?
- False. The standard deviation of \(X\) is about equal to \(1\) and is therefore smaller than \(6\).
- True. \(X\) and \(Y\) have both mean \(0\) and variance \(1\).
- False. The regression line at \(X=-0.6\) implies a value of about \(Y = -0.6\).
- True. The mean of \(X\) is about equal to \(0\) and hence is smaller than \(5\).
- False. A strong association between the variables is given in the scatterplot. Hence the absolute value of the correlation coefficient is close to \(1\) and therefore larger than \(0.8\).
Description:
Scatterplot in an (x, y) regression setup needs to be interpreted regarding location/spread of the marginal distributions, the correlation in the joint distribution, and the corresponding regression slope. Data are drawn randomly from a suitable data-generating process so that each multiple-choice item is either about correct or clearly wrong.
Solution feedback:
Yes
Randomization:
Random numbers, text blocks, and graphics
Mathematical notation:
No
Verbatim R input/output:
No
Images:
Yes
Other supplements:
No
Demo code:
library("exams")
set.seed(403)
exams2html("scatterplot.Rmd")
set.seed(403)
exams2pdf("scatterplot.Rmd")
set.seed(403)
exams2html("scatterplot.Rnw")
set.seed(403)
exams2pdf("scatterplot.Rnw")