dist3: Distances and the Pythagorean Theorem (Single-Choice)
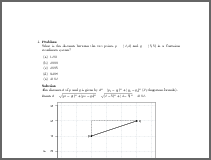
dist3What is the distance between the two points \(p = (2, 4)\) and \(q = (5, 5)\) in a Cartesian coordinate system?
The distance \(d\) of \(p\) and \(q\) is given by \(d^2 = (p_1 - q_1)^2 + (p_2 - q_2)^2\) (Pythagorean formula).
Hence \(d = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} = \sqrt{(2 - 5)^2 + (4 - 5)^2} = 3.162\).
- False
- False
- False
- False
- True
What is the distance between the two points \(p = (3, 5)\) and \(q = (5, 1)\) in a Cartesian coordinate system?
The distance \(d\) of \(p\) and \(q\) is given by \(d^2 = (p_1 - q_1)^2 + (p_2 - q_2)^2\) (Pythagorean formula).
Hence \(d = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} = \sqrt{(3 - 5)^2 + (5 - 1)^2} = 4.472\).
- False
- False
- False
- True
- False
What is the distance between the two points \(p = (3, 5)\) and \(q = (4, 2)\) in a Cartesian coordinate system?
The distance \(d\) of \(p\) and \(q\) is given by \(d^2 = (p_1 - q_1)^2 + (p_2 - q_2)^2\) (Pythagorean formula).
Hence \(d = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2} = \sqrt{(3 - 4)^2 + (5 - 2)^2} = 3.162\).
- False
- False
- False
- False
- True
num_to_schoice() by providing two common errors along with a range and minimal delta for two further random solutions.(Note that the HTML output contains mathematical equations in MathML, rendered by MathJax using ‘mathjax = TRUE’. Instead it is also possible to use ‘converter = “pandoc-mathjax”’ so that LaTeX equations are rendered by MathJax directly.)
Demo code:
library("exams")
set.seed(403)
exams2html("dist3.Rmd", mathjax = TRUE)
set.seed(403)
exams2pdf("dist3.Rmd")
set.seed(403)
exams2html("dist3.Rnw", mathjax = TRUE)
set.seed(403)
exams2pdf("dist3.Rnw")