dist2: Three Distances in a Cartesian Coordinate System

Exercise template for computing the Manhattan, Euclidean, and maximum distance (cloze with three numeric answers) between two randomly-drawn points in a Cartesian coordinate system.

Name:
dist2
Type:
cloze
Related:
dist, dist3
Preview:

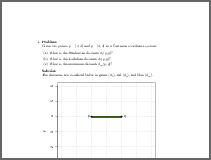
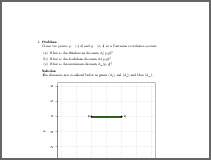
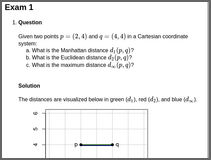
Given two points \(p = (2, 4)\) and \(q = (4, 4)\) in a Cartesian coordinate system:

What is the Manhattan distance \(d_1(p, q)\)?

What is the Euclidean distance \(d_2(p, q)\)?

What is the maximum distance \(d_\infty(p, q)\)?

The distances are visualized below in green (\(d_1\)), red (\(d_2\)), and blue (\(d_\infty\)).

  • \(d_1(p, q) = \sum_i |p_i - q_i| = |2 - 4| + |4 - 4| = 2\).
  • \(d_2(p, q) = \sqrt{\sum_i (p_i - q_i)^2} = \sqrt{(2 - 4)^2 + (4 - 4)^2} = 2\).
  • \(d_\infty(p, q) = \max_i |p_i - q_i| = \max(|2 - 4|, |4 - 4|) = 2\).

Given two points \(p = (3, 2)\) and \(q = (5, 5)\) in a Cartesian coordinate system:

What is the Manhattan distance \(d_1(p, q)\)?

What is the Euclidean distance \(d_2(p, q)\)?

What is the maximum distance \(d_\infty(p, q)\)?

The distances are visualized below in green (\(d_1\)), red (\(d_2\)), and blue (\(d_\infty\)).

  • \(d_1(p, q) = \sum_i |p_i - q_i| = |3 - 5| + |2 - 5| = 5\).
  • \(d_2(p, q) = \sqrt{\sum_i (p_i - q_i)^2} = \sqrt{(3 - 5)^2 + (2 - 5)^2} = 3.606\).
  • \(d_\infty(p, q) = \max_i |p_i - q_i| = \max(|3 - 5|, |2 - 5|) = 3\).

Given two points \(p = (3, 2)\) and \(q = (4, 1)\) in a Cartesian coordinate system:

What is the Manhattan distance \(d_1(p, q)\)?

What is the Euclidean distance \(d_2(p, q)\)?

What is the maximum distance \(d_\infty(p, q)\)?

The distances are visualized below in green (\(d_1\)), red (\(d_2\)), and blue (\(d_\infty\)).

  • \(d_1(p, q) = \sum_i |p_i - q_i| = |3 - 4| + |2 - 1| = 2\).
  • \(d_2(p, q) = \sqrt{\sum_i (p_i - q_i)^2} = \sqrt{(3 - 4)^2 + (2 - 1)^2} = 1.414\).
  • \(d_\infty(p, q) = \max_i |p_i - q_i| = \max(|3 - 4|, |2 - 1|) = 1\).
Description:
Computing three different distance measures between the same two randomly-drawn points by using Manhatten, Euclidean, and maximum distance.
Solution feedback:
Yes
Randomization:
Random numbers and graphics
Mathematical notation:
Yes
Verbatim R input/output:
No
Images:
Yes
Other supplements:
No
Template:
dist2.Rmd
dist2.Rnw
Raw: (1 random version)
dist2.md
dist2.tex
PDF:
dist2-Rmd-pdf
dist2-Rnw-pdf
HTML:
dist2-Rmd-html
dist2-Rnw-html

(Note that the HTML output contains mathematical equations in MathML, rendered by MathJax using ‘mathjax = TRUE’. Instead it is also possible to use ‘converter = “pandoc-mathjax”’ so that LaTeX equations are rendered by MathJax directly.)

Demo code:

library("exams")

set.seed(403)
exams2html("dist2.Rmd", mathjax = TRUE)
set.seed(403)
exams2pdf("dist2.Rmd")

set.seed(403)
exams2html("dist2.Rnw", mathjax = TRUE)
set.seed(403)
exams2pdf("dist2.Rnw")

TEMPLATES
cloze numeric arithmetic distance Euclidean Manhattan maximum mathematics