confint2: 2-Sided Confidence Interval
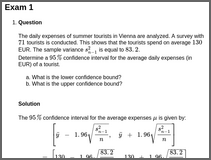
confint2The daily expenses of summer tourists in Vienna are analyzed. A survey with \(71\) tourists is conducted. This shows that the tourists spend on average \(130\) EUR. The sample variance \(s^2_{n-1}\) is equal to \(83.2\).
Determine a \(95\%\) confidence interval for the average daily expenses (in EUR) of a tourist.
What is the lower confidence bound?
What is the upper confidence bound?
The \(95\%\) confidence interval for the average expenses \(\mu\) is given by: \[ \begin{aligned} & & \left[\bar{y} \, - \, 1.96\sqrt{\frac{s_{n-1}^2}{n}}, \; \bar{y} \, + \, 1.96\sqrt{\frac{s_{n-1}^2}{n}}\right] \\ & = & \left[ 130 \, - \, 1.96\sqrt{\frac{83.2}{71}}, \; 130 \, + \, 1.96\sqrt{\frac{83.2}{71}}\right] \\ & = & \left[127.878, \, 132.122\right]. \end{aligned} \]
- The lower confidence bound is \(127.878\).
- The upper confidence bound is \(132.122\).
The daily expenses of summer tourists in Vienna are analyzed. A survey with \(79\) tourists is conducted. This shows that the tourists spend on average \(135\) EUR. The sample variance \(s^2_{n-1}\) is equal to \(161.1\).
Determine a \(95\%\) confidence interval for the average daily expenses (in EUR) of a tourist.
What is the lower confidence bound?
What is the upper confidence bound?
The \(95\%\) confidence interval for the average expenses \(\mu\) is given by: \[ \begin{aligned} & & \left[\bar{y} \, - \, 1.96\sqrt{\frac{s_{n-1}^2}{n}}, \; \bar{y} \, + \, 1.96\sqrt{\frac{s_{n-1}^2}{n}}\right] \\ & = & \left[ 135 \, - \, 1.96\sqrt{\frac{161.1}{79}}, \; 135 \, + \, 1.96\sqrt{\frac{161.1}{79}}\right] \\ & = & \left[132.201, \, 137.799\right]. \end{aligned} \]
- The lower confidence bound is \(132.201\).
- The upper confidence bound is \(137.799\).
The daily expenses of summer tourists in Vienna are analyzed. A survey with \(116\) tourists is conducted. This shows that the tourists spend on average \(131.6\) EUR. The sample variance \(s^2_{n-1}\) is equal to \(242.5\).
Determine a \(95\%\) confidence interval for the average daily expenses (in EUR) of a tourist.
What is the lower confidence bound?
What is the upper confidence bound?
The \(95\%\) confidence interval for the average expenses \(\mu\) is given by: \[ \begin{aligned} & & \left[\bar{y} \, - \, 1.96\sqrt{\frac{s_{n-1}^2}{n}}, \; \bar{y} \, + \, 1.96\sqrt{\frac{s_{n-1}^2}{n}}\right] \\ & = & \left[ 131.6 \, - \, 1.96\sqrt{\frac{242.5}{116}}, \; 131.6 \, + \, 1.96\sqrt{\frac{242.5}{116}}\right] \\ & = & \left[128.766, \, 134.434\right]. \end{aligned} \]
- The lower confidence bound is \(128.766\).
- The upper confidence bound is \(134.434\).
(Note that the HTML output contains mathematical equations in MathML, rendered by MathJax using ‘mathjax = TRUE’. Instead it is also possible to use ‘converter = “pandoc-mathjax”’ so that LaTeX equations are rendered by MathJax directly.)
Demo code:
library("exams")
set.seed(403)
exams2html("confint2.Rmd", mathjax = TRUE)
set.seed(403)
exams2pdf("confint2.Rmd")
set.seed(403)
exams2html("confint2.Rnw", mathjax = TRUE)
set.seed(403)
exams2pdf("confint2.Rnw")