anova: 1-Way Analysis of Variance
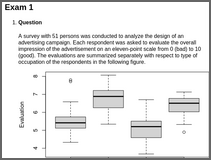
anovaA survey with 51 persons was conducted to analyze the design of an advertising campaign. Each respondent was asked to evaluate the overall impression of the advertisement on an eleven-point scale from 0 (bad) to 10 (good). The evaluations are summarized separately with respect to type of occupation of the respondents in the following figure.
To analyze the influence of occupation on the evaluation of the advertisement an analysis of variance was performed:
Res.Df RSS Df Sum of Sq F Pr(>F)
1 50 53.549
2 47 34.018 3 19.531 8.995 8.1265e-05Which of the following statements are correct?
In order to be able to answer the questions the fraction of explained variance has to be determined. The residual sum of squares when using only a single overall mean value (\(\mathit{RSS}_0\)) as well as the residual sum of squares when allowing different mean values given occupation (\(\mathit{RSS}_1\)) are required. Both are given in the RSS column of the ANOVA table. The fraction of explained variance is given by \(1 - \mathit{RSS}_1/\mathit{RSS}_0 = 1 - 34.018/53.549 = 0.365\).
The statements above can now be evaluated as right or wrong.
- True. The \(p\) value is \(8.13e-05\) and hence significant. It can be shown that the evaluations differ with respect to the occupation of the respondents.
- False. The fraction of explained variance is \(0.365\) and hence not larger than 0.6.
- False. An ANOVA always tests the null hypothesis, that all mean values are equal against the alternative hypothesis that they are different.
- True. The fraction of explained variance is \(0.365\) and hence smaller than 0.45.
- True. The test statistic is \(F = 8.995\) and hence larger than \(7.5\).
A survey with 48 persons was conducted to analyze the design of an advertising campaign. Each respondent was asked to evaluate the overall impression of the advertisement on an eleven-point scale from 0 (bad) to 10 (good). The evaluations are summarized separately with respect to type of occupation of the respondents in the following figure.
To analyze the influence of occupation on the evaluation of the advertisement an analysis of variance was performed:
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 53.615
2 44 27.809 3 25.806 13.611 2.04e-06Which of the following statements are correct?
In order to be able to answer the questions the fraction of explained variance has to be determined. The residual sum of squares when using only a single overall mean value (\(\mathit{RSS}_0\)) as well as the residual sum of squares when allowing different mean values given occupation (\(\mathit{RSS}_1\)) are required. Both are given in the RSS column of the ANOVA table. The fraction of explained variance is given by \(1 - \mathit{RSS}_1/\mathit{RSS}_0 = 1 - 27.809/53.615 = 0.481\).
The statements above can now be evaluated as right or wrong.
- True. The \(p\) value is \(2.04e-06\) and hence significant. It can be shown that the evaluations differ with respect to the occupation of the respondents.
- True. The fraction of explained variance is \(0.481\) and hence larger than 0.19.
- False. The test statistic is \(F = 13.611\) and hence not larger than \(23.1\).
- False. An ANOVA always tests the null hypothesis, that all mean values are equal against the alternative hypothesis that they are different.
- True. The fraction of explained variance is \(0.481\) and hence smaller than 0.51.
A survey with 53 persons was conducted to analyze the design of an advertising campaign. Each respondent was asked to evaluate the overall impression of the advertisement on an eleven-point scale from 0 (bad) to 10 (good). The evaluations are summarized separately with respect to type of occupation of the respondents in the following figure.
To analyze the influence of occupation on the evaluation of the advertisement an analysis of variance was performed:
Res.Df RSS Df Sum of Sq F Pr(>F)
1 52 33.596
2 49 32.416 3 1.180 0.594 0.62163Which of the following statements are correct?
In order to be able to answer the questions the fraction of explained variance has to be determined. The residual sum of squares when using only a single overall mean value (\(\mathit{RSS}_0\)) as well as the residual sum of squares when allowing different mean values given occupation (\(\mathit{RSS}_1\)) are required. Both are given in the RSS column of the ANOVA table. The fraction of explained variance is given by \(1 - \mathit{RSS}_1/\mathit{RSS}_0 = 1 - 32.416/33.596 = 0.035\).
The statements above can now be evaluated as right or wrong.
- False. An ANOVA always tests the null hypothesis, that all mean values are equal against the alternative hypothesis that they are different.
- False. The \(p\) value is \(0.622\) and hence_not_ significant. It can not be shown that the evaluations differ with respect to the occupation of the respondents.
- True. The fraction of explained variance is \(0.035\) and hence smaller than 0.12.
- False. The test statistic is \(F = 0.594\) and hence not larger than \(3.2\).
- False. The fraction of explained variance is \(0.035\) and hence not larger than 0.13.
(Note that the HTML output contains mathematical equations in MathML, rendered by MathJax using ‘mathjax = TRUE’. Instead it is also possible to use ‘converter = “pandoc-mathjax”’ so that LaTeX equations are rendered by MathJax directly.)
Demo code:
library("exams")
set.seed(403)
exams2html("anova.Rmd", mathjax = TRUE)
set.seed(403)
exams2pdf("anova.Rmd")
set.seed(403)
exams2html("anova.Rnw", mathjax = TRUE)
set.seed(403)
exams2pdf("anova.Rnw")